Fakultät in Prolog. Das Programm und die Lösungssuche als Suchbaum
Eine Präsentation von Philipp Hauer vom 18.10.2007. Erstmals gehalten am Richard-Wossidlo-Gymnasium am 12.10.2007. ©
Inhalt
Die Fakultät !
"Die Fakultät [...] ist [...] eine Funktion, die einer natürlichen Zahl das Produkt aller natürlichen Zahlen kleiner oder gleich dieser Zahl zuordnet" (Quelle: Wikipedia, Stand: 18.10.07). Dazu einige selbsterkärende Beispiele:
0! = 1
1! = 1 = 1
2! = 1*2 = 2
3! = 1*2*3 = 6
4! = 1*2*3*4 = 24
5! = 1*2*3*4*5 = 120
6! = 1*2*3*4*5*6 = 720
Hinweis: Besonders wichtig dabei ist die Fakultät 0! = 1. Diese spielt im Prolog-Programm später eine entscheidene Rolle.
Damit gilt der allgemeine Fall:
| 0! = 1 | (Abbruchbedingung) |
| n! = n * (n - 1)!; n > 0 | (rekursiver Fall) |
Umsetzung in Java
Zum Vergleich, die Umsetzung der Fakultät in einer imperativen Programmiersprache (hier Java). Der Methode wird die auszurechnende Fakultät in Form von n übergeben.
public int fakultaet(int n){
int m = n - 1;
while(m>0){
n = n*m;
m--;
}
return n;
}
Ohne tief in den Code einzusteigen, sehen wir 3 Grundelemente, die wir auch in Prolog wiederfinden werden: Es wird eine zweite (lokale) Variable m initiierte, die den Wert n-1 hat. Nun wird in einer Schleife n*m gerechnet bis m=0 ist, wobei m bei jedem Schleifendurchgang um 1 vermindert wird. Diese Grundelemente Subtraktion, Multiplikation und Schleife (in Prolog realisiert durch Rekursion) finden wir auch in Prolog.
Umsetzung in Prolog
Nun werfen wir endlich einen Blick auf das Programm in Prolog. Gelesen wird: fak(N,F) --> N! = F.
fak(0, 1).
|
--> Abbruchbedingung/Rekursionsausstieg
--> Rekursiver Fall: --> Rekursion, Rückbezug auf Definition |
Wie erwartet handelt es sich um eine Rekursion. Der Rekursionsausstieg ist das Faktum fak(0,1). Mit der rekursiven Regel fak(N,F) wird versucht, die Anfrage auf diese Abbruchbedingung schrittweise zu reduzieren, um die davon ausgehen zu lösen. In ihr finden wir wie auch in Java unsere Subtraktion mit einer neuen Variablen (N1) als Ergebnis und die Multiplikation. Jedoch findet die Rekursion fak(N1,F1) vor der Multiplikation statt. Wir können also schließen, dass zuerst N schrittweise um 1 reduziert wird bis der Ausdruck unifizierbar mit dem Faktum fak(0,1) ist. Erst dann (mit F = 1) beginnt die Multiplikation mit dem nun zunehmenden (da rückwärts ausgeführt) N; Prolog baut sich wahre Fakultäten schrittweise auf bis er bei der gesuchten angelangt ist. Wie genau das abläuft, sehen wir ausführlich im Suchbaum.
Leistungen
Das Programm kann Entscheidungsfragen beantworten. So liefert es bei der Anfrage ?- fak(3,6) yes zurück. Jedoch kann es Ergänzungsfragen nur bedingt beantworten. Es kann die Fakultät F aus einer gegebenen Zahl N errechnen (z. B.: ?- fak(3,F) --> F = 6), jedoch funktioniert der umgekehrte Weg nicht (?- fak(N,6) --> n. l./error).
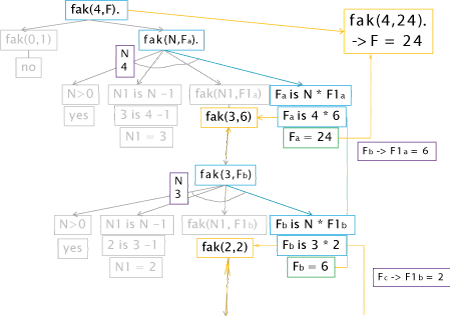
Die Lösungssuche als Suchbaum
 |
Zur besseren Veranschaulichung wurde der Suchbaum zerteilt, damit Bild und Text sich besser ergänzen. Den ganzen Suchbaum gibt es |
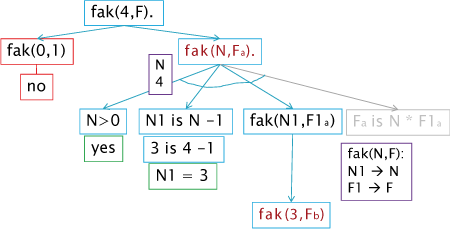
An Prolog stellen wir die Ergänzungsfrage fak(4,F). Wir wollen F = 4! zurückerhalten.
Prolog versucht zuerst die Anfrage mit einem Fakt aus der Datenbasis zu lösen (genauer zu unifizieren). Da nur fak(0,1) definiert ist, gelingt dies nicht (N = 0 ± 4). Somit geht Prolog in die rekursive Regel mit N = 4. Die erste Bedingung N>0 (4>0) wird bestanden und zum nächsten Befehl N1 is N - 1 gegangen: 3 = 4 - 1; N1 = 3.
Jetzt ist Prolog zum ersten Mal bei der Rekursion fak(N1,F1) angelangt. Der letzte Schritt F is N * F1 wird damit vorerst "ausgelassen". Durch die Rekursion wird aus der Regel vorzeitig ausgestiegen und Prolog beginnt die Lösungssuche wieder "von oben", wobei nun N = 3 ist. Die Variablen N1 bzw. F1 wurden dazu unifiziert (gleichgesetzt) zu N bzw. F, sodass man wieder zum Ausgangsausdruck fak(N,F) bzw. fak(3,F) gelangt.
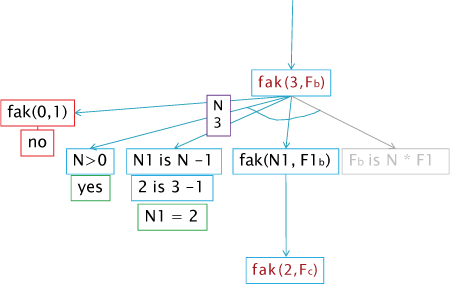
Die Schrittfolge wiederholt sich nun. Wieder gibt es für fak(3,F) keinen matchenden Fakt in der Datenbasis, sodass in die rekursive Regel gegangen wird. Dort wird die Bedingung N>0 (3>0) bestanden und N1 aus N - 1 (2 = 3 - 1) errechnet. Die Rekursion wiederholt sich nun mit N = 2.
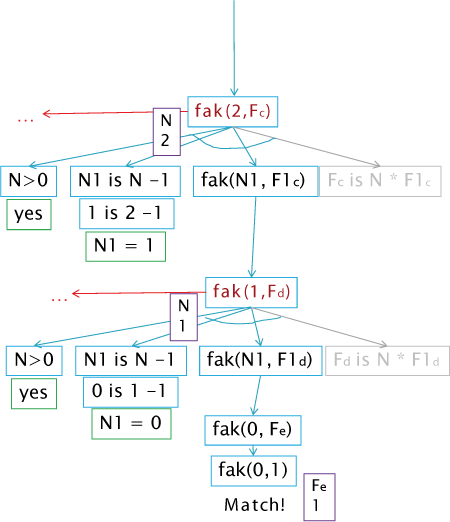
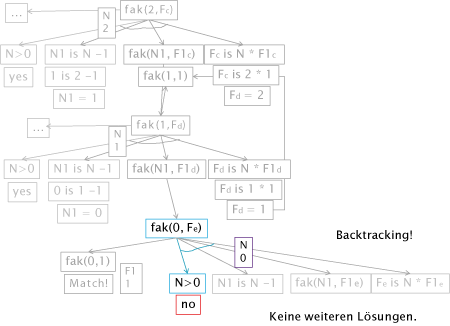
Dieser Vorgang wird dann noch einmal mit N = 2 und dann mit N = 1 durch prozessiert bis am Ende die letzte Rekursion mit fak(0,F) beginnt. Hier findet Prolog nun endlich ein unifizierbaren Fakt fak(0,1), unseren Rekursionsausstieg/unserer Abbruchbedingung. Es matcht und endlich kann Prolog die Variable F mit 1 belegen. Auf dieses Ergebnis zielte die gesamte Rekursion ab.
Jetzt beginnt der "Rückweg": der Weg aus den Rekursionen zurück zur ursprünglichen Anfrage.
Die mit 1 belegte Variable F wird "zurückunifiziert" zu F1. Damit wurde die Bedingung fak(N1,F1) mit F1 = 1 erfüllt bzw. abgearbeitet - der ursprüngliche Grund für die Rekursion. Jetzt kann Prolog endlich den letzten Schritt F is N * F1 gehen. In der vorletzten Ebene/vorletzten Rekursion ist N = 1, daher ergibt sich die Rechnung F is 1 * 1; F erhält den Wert 1.
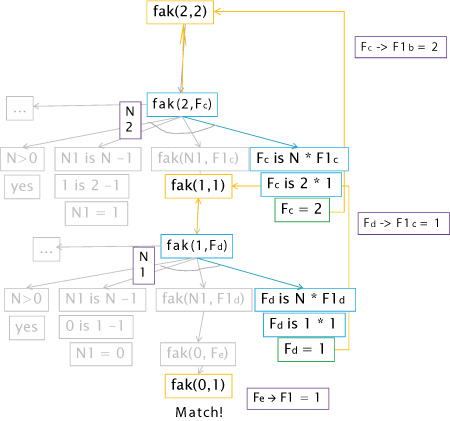
Da F nun mit 1 belegt werden konnte, wird in der Ebene/Rekursion darüber ebenso die Bedingung fak(N1,F1) abgearbeitet werden. Ergebnis nach Rückunifikation der Variablen N -> N1 und F -> F1: fak(1,1). Wieder ist in dieser Ebene nun F1 als Wert (1) verfügbar und wird mit N (hier 2) multipliziert: 2 is 1 * 1 --> F = 2.
Eine Rekursion/Ebene darüber ist nun F1 (= 2) in fak(N1,F1) --> fak(2,2) verfügbar.
Zwischenbilanz: Prolog baut sich gewissermaßen seine Fakultät schrittweise auf bis er bei der gewünschten Größe (N = 4) ankommt. Besonders hervorzuheben sind die wahren Aussagen auf die Prolog dabei kommt: fak(0,1), fak(1,1), fak(2,2) und - wie wir gleich sehen werden - fak(3,6) und schließlich fak(4,24).
Hinweis: Wir sehen also, dass Prolog nicht wirklich den Rückweg antritt, sondern lediglich weiterarbeitet. Die Rekursion war nur Mittel zum Zweck, um für F1 einen Wert zu erhalten, danach beginnt der Weg aus den Rekursionen schrittweise zurück zur Ausgangsanfrage.
Die letzten Schritte in Kürze: F is N * F1, wobei F1 = 2 und N = 3 ist. 3*2 = 6 = F. Ergebnis der Rekursion: fak(3,6).
Wir nähern uns dem ursprünglichen Ziel (4!): F1 = 6 und N = 4; multipliziert ergeben sie F = 24. Prolog ist damit bei seinem Ergebnis angelangt: fak(4,24) --> F = 24 und gibt dieses aus.
Doch Prolog ist noch nicht fertig. Es könnten ja noch mehr Lösungen geben. Das Backtracking (= das Fortsetzen der Lösungssuche am letzten Alternativpunkt) beginnt. Dabei wird F, welches beim ersten Durchgang mit 1 belegt wurde, wieder frei. Auf der Suche nach weiteren Lösungen arbeitet Prolog stupide weiter und geht in die rekursive Regel fak(N,F). Doch dort scheitert er bereits an der ersten Bedingung N>0, da N = 0 ist. Das System liefert fail zurück und beendet damit die Lösungssuche endgültig mit der Erkenntnis, dass es keine weiteren Lösungen gibt. Klar: Zu 4! gibt es nur ein Ergebnis.
Der Trace-Modus im Prolog Editor
Was genau Prolog während der Lösungssuche macht, sehen wir noch einmal im Trace-Modus des SWI Prolog Editors:
| [trace] 3 ?- fak(4,F).
Call: (7) fak(4, _G417) ? Call: (8) 4>0 ? Exit: (8) 4>0 ? Call: (8) _L172 is 4-1 ? Exit: (8) 3 is 4-1 ? Call: (8) fak(3, _L173) ? Call: (9) 3>0 ? Exit: (9) 3>0 ? Call: (9) _L191 is 3-1 ? Exit: (9) 2 is 3-1 ? Call: (9) fak(2, _L192) ? Call: (10) 2>0 ? Exit: (10) 2>0 ? Call: (10) _L210 is 2-1 ? Exit: (10) 1 is 2-1 ? Call: (10) fak(1, _L211) ? Call: (11) 1>0 ? Exit: (11) 1>0 ? Call: (11) _L229 is 1-1 ? Exit: (11) 0 is 1-1 ? Call: (11) fak(0, _L230) ? Exit: (11) fak(0, 1) ? |
Call: (11) _L211 is 1*1 ?
Exit: (11) 1 is 1*1 ? Exit: (10) fak(1, 1) ? Call: (10) _L192 is 2*1 ? Exit: (10) 2 is 2*1 ? Exit: (9) fak(2, 2) ? Call: (9) _L173 is 3*2 ? Exit: (9) 6 is 3*2 ? Exit: (8) fak(3, 6) ? Call: (8) _G417 is 4*6 ? Exit: (8) 24 is 4*6 ? Exit: (7) fak(4, 24) ? F = 24 ; Redo: (11) fak(0, _L230) ? Call: (12) 0>0 ? Fail: (12) 0>0 ? Fail: (10) fak(1, _L211) ? Fail: (9) fak(2, _L192) ? Fail: (8) fak(3, _L173) ? Fail: (7) fak(4, _G417) ? No |
Das Prinzip
Fassen wir noch einmal das Prinzip des Programms zur Berechnung der Fakultät zusammen:
Rekursionsabstieg: Auf dem Hinweg wird N in N Schritten je um 1 vermindert, um es schließlich auf den einfachen Fall fak(0,1) zu reduzieren:
4 -> 3 -> 2 -> 1 -> 0
Rekursionsaufstieg: Auf dem "Rückweg" (dem Weg aus den Rekursionen zurück zur Ausgangsanfrage) wird das zunehmende N in N Multiplikationen mit dem Ergebnis von N*F1 multipliziert:
1*1=1 -> 2*1=2 -> 3*2=6 -> 4*6=24
Die Powerpoint-Präsentation
Diesen Artikel gibt es auch als Powerpoint-Präsentation. Diese bietet Animationen und besondere Veranschaulichung: so ist der Suchbaum auf einer Folie mit dem Trace-Modus und dem Quellcode. Hier geht es zum Download: Fakultät in Prolog: Das Programm und der Suchbaum (ppt; 2,26 MB).